Построение фигур одним росчерком карандаша
I. Постановка проблемной ситуации.
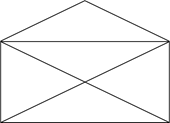
Наверное, все помнят с детства, что очень популярна была следующая задача: не отрывая карандаша от бумаги и не проводя по одной линии дважды, начертить “открытый конверт”:
Попробуйте нарисовать “открытый конверт”.
Как вы видите, что у некоторых получается, а у некоторых нет. Почему это происходит? Как правильно рисовать, чтобы получилось? И для чего она нужна? Чтобы ответить на эти вопросы, я расскажу вам, один исторический факт.
Город Кенигсберг (после мировой войны он называется Калининград) стоит на реке Преголь. Некогда там было 7 мостов, которые связывали между собой берега и два острова. Жители города заметили, что они никак не могут совершить прогулку по всем семи мостам, пройдя по каждому из них ровно один раз. Так возникла головоломка: “можно ли пройти все семь кенигсбергских мостов ровно один раз и вернуться в исходное место?”.
Попробуйте и вы, может у кого-нибудь получится.
В 1735 году эта задача стала известна Леонарду Эйлеру. Эйлер выяснил, что такого пути нет, т. е. доказал, что эта задача неразрешима. Конечно, Эйлер решил не только задачу о кенигсбергский мостах, а целый класс аналогичных задач, для которых разработал метод решения. Можно заметить, что задача состоит в том, чтобы по карте провести маршрут – линию, не отрывая карандаша от бумаги, обойти все семь мостов и вернуться в начальную точку. Поэтому Эйлер стал рассматривать вместо карты мостов схему из точек и линий, отбросив мосты, острова и берега, как не математические понятия. Вот что у него получилось:
А, В – острова, M, N – берега, а семь кривых – семь мостов.
Теперь задача такая – обойти контур на рисунке так, чтобы каждая кривая проводилась ровно один раз.
В наше время такие схемы из точек и линий стали называть графами, точки называют вершинами графа, а линии – ребрами графа. В каждой вершине графа сходится несколько линий. Если число линий четно, то вершина называется четная, если число вершин нечетно, то вершина называется нечетной.
Докажем неразрешимость нашей задачи.
Как видим, в нашем графе все вершины нечетные. Для начала докажем, что, если обход графа начинается не с нечетной точки, то он обязательно должен закончится в этой точке
Рассмотрим для примера вершину с тремя линиями. Если мы по одной линии пришли, по другой вышли, и по третьей опять вернулись. Все дальше идти некуда ( ребер больше нет). В нашей задаче мы сказали, что все точки нечетные, значит, выйдя из одной из них, мы должны закончить сразу в трех остальных нечетных точках, чего не может быть.
До Эйлера ни кому в голову не приходило, что головоломка о мостах и другие головоломки с обходом контура, имеет отношение к математике. Анализ Эйлера таких задач “является первым ростком новой области математики, сегодня известной под названием топология”.
Топология – это раздел математики, изучающий такие свойства фигур, которые не меняются при деформациях, производимых без разрывов и склеивания.
Например, с точки зрения топологии, круг, эллипс, квадрат и треугольник обладают одинаковыми свойствами и являются одной и той же фигурой, так как можно деформировать одну в другую, а вот кольцо к ним не относится, так как, чтобы его деформировать в круг, необходима склейка.
II. Признаки вычерчивания графа.
1. Если в графе нет нечетных точек, то ее можно нарисовать одним росчерком, не отрывая карандаша от бумаги, начиная с любого места.
2. Если в графе две нечетные вершины, то ее можно начертить одним росчерком, не отрывая карандаша от бумаги, причем вычерчивать нужно начинать в одной нечетной точке, а закончить в другой.
3. Если в графе более двух нечетных точек, то ее нельзя начертить одним росчерком карандаша.
Вернемся к нашей задаче с открытым конвертом. Подсчитаем количество четных и нечетных точек: 2 нечетные и 3 четные, значит, эту фигуру можно начертить одним росчерком, причем начать нужно в нечетной точке. Попробуйте, теперь у всех получилось?
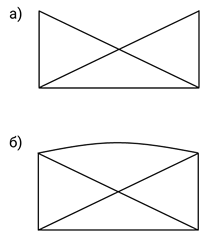
Закрепим полученные знания. Определите, какие фигуры можно построить, а какие нельзя.
а) Все точки четные, поэтому эту фигуру можно построить, начиная с любого места, например:
б) В этой фигуре две нечетные точки, поэтому ее можно построить не отрывая, карандаша от бумаги, начиная с нечетной точки.
в) В этой фигуре четыре нечетные точки, поэтому ее нельзя построить.
г) Здесь все точки четные, поэтому ее можно построить, начиная с любого места.
Проверим, как вы усвоили новые знания.
III. Самостоятельная работа по карточкам с индивидуальными заданиями.
Задание: проверить, можно ли совершить прогулку по всем мостам, пройдя по каждому из них ровно один раз. И если можно, то нарисовать путь.
Источник
Вычерчивание фигур одним росчерком
Урок 29. Математика и игры 3–4 классы

Конспект урока «Вычерчивание фигур одним росчерком»
Посмотрите на эту фигуру:
Она похожа на открытый конверт.
Наверное, многие из вас раньше пробовали нарисовать такой конверт, не отрывая карандаш от бумаги и не проводя больше одного раза по одной и той же линии.
У кого-то это получалось, а у кого-то – нет.
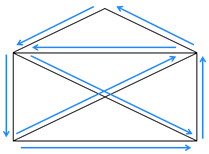
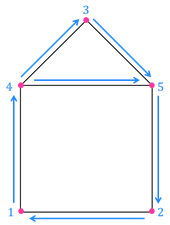
Вообще, эту фигуру можно нарисовать одним росчерком, если проводить линии, например, вот в такой последовательности.
Обратите внимание, что не было проведено дважды ни по одной из линий фигуры.
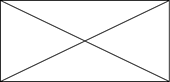
А теперь посмотрите вот на такую фигуру:
Эта фигура напоминает закрытый конверт.
На первый взгляд данная фигура кажется более простой, ведь она содержит меньше линий. Но вот нарисовать её, не отрывая карандаш от бумаги и не проводя никакой линии дважды, у нас не получится.
Почему какие-то фигуры получается нарисовать, не отрывая карандаш от бумаги и не проводя никакую линию больше одного раза, а какие-то – нет?
Давайте разберёмся. Посмотрите на рисунок, который создан при помощи нескольких линий. Такие рисунки ещё называют графами.
Вы, наверное, слышали, что словом «граф» называют богатого и знатного человека в старинных романах. Однако в математике граф – это рисунок, созданный при помощи прямых линий, образующих углы.
«Граф» в переводе с греческого означает «пишу». Точки, в которых соединяются линии графа, называются узлами.
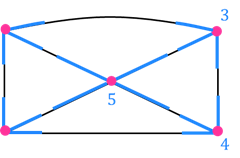
В нашем графе пять узлов.
Посмотрите, в первом, втором и третьем узлах соединяется по 2 линии. То есть чётное число. Поэтому эти узлы называются чётными.
А вот в четвёртом и пятом узлах соединяется по 3 линии. То есть нечётное число. Поэтому эти узлы называются нечётными.
Получается, что в этом графе 3 чётных узла и 2 нечётных.
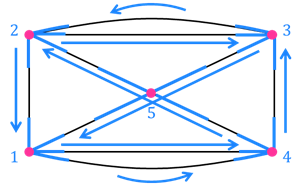
Попробуем нарисовать данную фигуру одним росчерком, то есть, не отрывая карандаш от бумаги и не проводя никакую линию дважды.
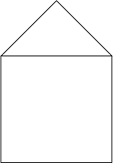
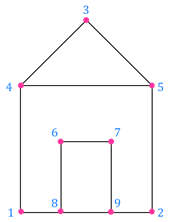
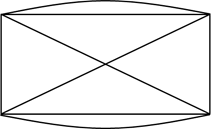
Теперь посмотрите на фигуру, которая похожа на домик с дверью.
В первом, втором, третьем, шестом и седьмом узлах соединяется по 2 линии. А значит, эти узлы являются чётными.
В четвёртом, пятом, восьмом и девятом узлах соединяется по 3 линии. А значит, эти узлы являются нечётными.
Получается, что в этом графе 5 чётных узлов и 4 нечётных.
Надо отметить, что нечётных узлов здесь больше двух.
Запомните! Если в фигуре (на графе) число нечётных узлов больше двух, то её нельзя нарисовать одним росчерком.
Значит, фигуру в виде домика с дверью нельзя нарисовать одним росчерком. Ведь у этой фигуры целых 4 нечётных узла.
А сейчас давайте выполним несколько заданий.
Задание первое. Выясните, какие из фигур можно вычертить, не отрывая карандаш от бумаги и не проводя больше одного раза по одной и той же линии.
А догадался ли кто-нибудь из вас, что те фигуры, которые можно нарисовать одним росчерком, можно сделать и сгибанием из одного куска проволоки?
Задание второе. Можно ли из одного куска проволоки получить фигуру, которая изображена на рисунке?
Задание третье. Выясните, можно ли нарисовать фигуру, которая изображена на рисунке, не отрывая карандаш от бумаги и не проводя более одного раза ни одной линии.
Источник
Разбор головоломок: графы – фигуры одним росчерком и поиск пути
С давних пор известны и пользуются популярностью головоломки, которые можно объединить под общим названием «одним росчерком». В таких задачах предлагается начертить какую-либо фигуру одним росчерком (одной линией), не отрывая карандаша от бумаги, и не проводя дважды по одной линии. Классическими примерами являются задачи, в которых одним росчерком нужно нарисовать разные варианты конверта или квадрат с диагоналями и четырьмя дугами:
Вариантом задачи является поиск пути по дорогам или мостам, который будет проходить по всем дорогам (мостам) ровно по одному разу. Классическим примером является задача о семи кёнигсбергских мостах, которая опубликована на этой неделе под номером 5.
Также известна старая задача о доме из пяти комнат, каждая из которых соединена с другой и с улицей дверьми. Необходимо найти такой путь по комнатам, который проходил бы по всем 16 дверям ровно по одному разу (начинать и заканчивать можно в любой комнате или вне дома):
Независимо от условий задачи (начертить фигуру одной линией или найти непрерывный путь), ее решением является граф – математический объект, объединяющий в себе множество вершин и ребер. Причем как само понятие графа, так и раздел математики, изучающий данные объекты (он назван теорией графов), родились как раз из решения такой задачи. А именно – из решения задачи о семи кёнигсбергских мостах, которой в 1736 году занялся великий математик Леонард Эйлер. Правда, само понятие «граф» было предложено в 1878 году английским математиком Джеймсом Джозефом Сильвестром. Однако «отцом» теории графов по праву считается Эйлер, и здесь мы проследим за некоторыми его рассуждениями.
Правила Эйлера
При анализе задачи о мостах Кёнигсберга Эйлер преобразует карту города в упрощенную схему, в которой четыре части города превращаются в вершины, а мосты – в ребра, соединяющие эти вершины. Процесс преобразования можно проиллюстрировать картинкой:
Вот так Эйлер получил граф – абстрактный математический объект, состоящий из вершин, попарно соединенных ребрами. Вершины обозначены здесь красными точками, а ребра – черными линиями. А что за цифры стоят у вершин? О, это – как раз то, что и помогает решать любые (повторяю – любые) задачи о рисовании фигур одним росчерком! Это – обозначение четности/нечетности вершины, которое указывает на число ребер, которое выходит из данной вершины. Если из вершины выходит четное число ребер – значит она четная, а если нечетное – она нечетная. Все очень просто.
В ходе работы над задачей Эйлер вывел несколько заключений, в которых ключевую роль играет четность/нечетность вершин. Мы приведем здесь только те заключения, которые потребуются для решения головоломок:
- Если все вершины графа четные, то его можно начертить одним росчерком, не отрывая карандаша от бумаги. При этом можно начинать с любой вершины графа, а завершаться он будет в этой же точке;
- Если ровно две вершины графа нечетные, то его можно начертит одним росчерком, не отрывая карандаша от бумаги. При этом начать следует с одной из нечетных вершин, а завершать – во второй нечетной вершине;
- Если в графе три и больше нечетных вершин, то его невозможно начертить одним росчерком, не отрывая карандаша от бумаги, и не проводя по одному ребру дважды.
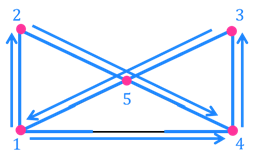
Итак, вновь посмотрим на граф задачи мостов Кёнигсберга: здесь четыре вершины, и все они нечетные. Значит, задача не имеет решения – пройти по всем семи мостам, посетив каждый из них ровно по одному разу, невозможно. Задача становится разрешимой только при добавлении одного моста (что в 1905 году и было сделано в реальности). Это можно сделать подобным образом (дополнительный мост указан пунктирной линией):
Как видите, в этом графе ровно две нечетных вершины, значит его можно начертить одним росчерком, не отрывая карандаша от бумаги, и не проводя по одной линии дважды. Но для этого следует начать в одной из нечетных вершин, и закончить в другой.
Анализ и решение задач
Теперь проанализируем фигуры, приведенные в начале статьи – конверты и квадрат с дугами:
Источник