Алгоритм Брезенхема для рисования наклонных отрезков
Алгоритм Брезенхема был предложен Джеком Е. Брезенхэмом (Jack E. Bresenham) в 1962 году и предназначен для рисования фигур точками на плоскости. Этот алгоритм находит широкое распространение в машинной графике для рисования линий на экране. Алгоритм определяет, какие точки двумерного растра необходимо закрасить.
Графическая интерпретация алгоритма Брезенхема представлена на рисунке.
Для рисования прямых отрезков на плоскости с использованием алгоритма Брезенхема запишем уравнение прямой в общем виде
y=kx+b
f(x,y)=Ax+By+C=0
где коэффициенты A и B выражаются через коэффициенты k и b уравнения прямой. Если прямая проходит через две точки с координатами (x1;y1) и (x2;y2) , то коэффициенты уравнения прямой определяются по формулам
A=y2-y1
B=x1-x2
C=y1∙x2-y2∙x1
Для любой растровой точки с координатами (xi;yi) значение функция
- f(xi,yi)=0 если точка лежит на прямой
- f(xi,yi)>0 если точка лежит ниже прямой
- f(xi,yi) где i – номер отображаемой точки.
Таким образом, одним из методов решения того, какая из точек P или Q (см. рисунок) будет отображена на следующем шаге, является сравнение середины отрезка |P-Q| со значением функции f(x,y) . Если значение f(x,y) лежит ниже средней точки отрезка |P-Q| , то следующей отображаемой точкой будет точка P , иначе — точка Q .
Запишем приращение функции
∆f=A∆x+B∆y
После отображения точки с координатами (xi,yi) принимается решение о следующей отображаемой точке. Для этого сравниваются приращения Δx и Δy , характеризующие наличие или отсутствие перемещения по соответствующей координате. Эти приращения могут принимать значения 0 или 1. Следовательно, когда мы перемещаемся от точки вправо,
∆f=A,
когда мы перемещаемся от точки вправо и вниз, то
∆f=A+B,
когда мы перемещаемся от точки вниз, то
∆f=B
Нам известны координаты начала отрезка, то есть точки, заведомо лежащей на искомой прямой. Ставим туда первую точку и принимаем f = 0 . От текущей точки можно сделать два шага — либо по вертикали (по горизонтали), либо по диагонали на один пиксель.
Направление движения по вертикали или горизонтали определяется коэффициентом угла наклона. В случае если угол наклона меньше 45º, и
|A| Реализация на C++
Алгоритм Брезенхема также может применяться в задачах управления, например, для регулирования мощности или скорости вращения. При этом горизонтальной осью является ось времени, а заданное значение устанавливает коэффициент угла наклона прямой.
Источник
Метод брезенхема для рисования окружности
Алгоритмы взяты из прекрасной книги
П.В.Вельтмандер «Машинная графика»
Во многих областях приложений, таких как, например, системы автоматизированного проектирования машиностроительного направления, естественными графическими примитивами, кроме отрезков прямых и строк текстов, являются и конические сечения, т.е. окружности, эллипсы, параболы и гиперболы. Наиболее употребительным примитивом, естественно, является окружность. Один из наиболее простых и эффективных алгоритмов генерации окружности разработан Брезенхемом.
1 Алгоритм Брезенхема


Для простоты и без ограничения общности рассмотрим генерацию 1/8 окружности, центр которой лежит в начале координат. Остальные части окружности могут быть получены последовательными отражениями (использованием симметрии точек на окружности относительно центра и осей координат).
Окружность с центром в начале координат описывается уравнением:
|
Алгоритм Брезенхема пошагово генерирует очередные точки окружности, выбирая на каждом шаге для занесения пиксела точку растра Pi(Xi, Yi), ближайшую к истинной окружности, так чтобы ошибка:
|
была минимальной. Причем, как и в алгоритме Брезенхема для генерации отрезков, выбор ближайшей точки выполняется с помощью анализа значений управляющих переменных, для вычисления которых не требуется вещественной арифметики. Для выбора очередной точки достаточно проанализировать знаки.
Рассмотрим генерацию 1/8 окружности по часовой стрелке, начиная от точки X=0, Y=R.
Проанализируем возможные варианты занесения i+1-й точки, после занесения i-й.
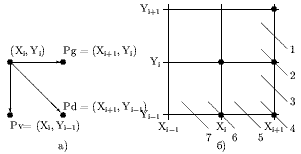
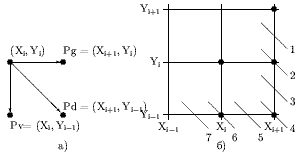
При генерации окружности по часовой стрелке после занесения точки (Xi, Yi) следующая точка может быть (см. рис. 0.1а) либо Pg = (Xi+1, Yi) — перемещение по горизонтали, либо Pd = (Xi+1, Yi-1) — перемещение по диагонали, либо Pv = (Xi, Yi-1) — перемещение по вертикали.
Для этих возможных точек вычислим и сравним абсолютные значения разностей квадратов расстояний от центра окружности до точки и окружности:
| ||||||||||||||||||||||||||||||||||||||||
Выбирается и заносится та точка, для которой это значение минимально.
Выбор способа расчета определяется по значению Dd. Если Dd 0, то диагональная точка вне окружности. Это варианты 5-7. И, наконец, если Dd = 0, то диагональная точка лежит точно на окружности. Это вариант 4. Рассмотрим случаи различных значений Dd в только что приведенной последовательности.
Случай Dd
Здесь в качестве следующего пиксела могут быть выбраны или горизонтальный — Pg или диагональный — Pd.
Для определения того, какой пиксел выбрать Pg или Pd составим разность:
| |||||||||
И будем выбирать точку Pg при di Ј 0, в противном случае выберем Pd.
Рассмотрим вычисление di для разных вариантов.
Для вариантов 2 и 3:
Dg і 0 и Dd
|
Добавив и вычтя (Y-1) 2 получим:
|
В квадратных скобках стоит Dd, так что
|
Для варианта 1:
Ясно, что должен быть выбран горизонтальный пиксел Pg. Проверка компонент di показывает, что Dg Случай Dd > 0
Здесь в качестве следующего пиксела могут быть выбраны или диагональный — Pd или вертикальный Pv.
Для определения того, какую пиксел выбрать Pd или Pv составим разность:
| |||||||||
Если si Ј 0, то расстояние до вертикальной точки больше и надо выбирать диагональный пиксел Pd, если же si > 0, то выбираем вертикальный пиксел Pv.
Рассмотрим вычисление si для разных вариантов.
Для вариантов 5 и 6:
Dd > 0 и Dv Ј 0, так как диагональный пиксел вне, а вертикальный либо вне либо на окружности.
|
Добавив и вычтя (X+1) 2 получим:
|
В квадратных скобках стоит Dd, так что
|
Для варианта 7:
Ясно, что должен быть выбран вертикальный пиксел Pv. Проверка компонент si показывает, что Dd > 0 и Dv > 0, причем si > 0, так как диагональная точка больше удалена от окружности, т.е. по критерию si > 0 как и в предыдущих случаях следует выбрать вертикальный пиксел Pv, что соответствует выбору для вариантов 5 и 6.
Случай Dd = 0
Для компонент di имеем: Dg > 0 и Dd = 0, следовательно по критерию di > 0 выбираем диагональный пиксел.
С другой стороны, для компонент si имеем: Dd = 0 и Dv Ј 0 также выбираем диагональный пиксел.
Dd Ј 0 — выбор горизонтального пиксела Pg
di > 0 — выбор диагонального пиксела Pd
si Ј 0 — выбор диагонального пиксела Pd
si > 0 — выбор вертикального пиксела Pv
выбор диагонального пиксела Pd.
Выведем рекуррентные соотношения для вычисления Dd для (i+1)-го шага, после выполнения i-го.
1. Для горизонтального шага к Xi+1, Yi
2. Для диагонального шага к Xi+1, Yi-1
3. Для вертикального шага к Xi, Yi-1
В Приложении 5 приведена подпрограмма V_circle, реализующая описанный выше алгоритм и строящая дугу окружности в первой четверти. Начальная инициализация должна быть:
Dd = (X+1) 2 + (Y-1) 2 — R 2 = 1 + (R-1) 2 — R 2 = 2*(1 — R)
Пикселы в остальных четвертях можно получить отражением. Кроме того достаточно сформировать дугу только во втором октанте, а остальные пикселы сформировать из соображений симметрии, например, с помощью подпрограммы Pixel_circle, приведенной в Приложении и заносящей симметричные пикселы по часовой стрелке от исходного.
В Приложении приведены подпрограмма V_BRcirc, реализующая описанный выше алгоритм и строящая дугу окружности во втором октанте с последующим симметричным занесением пикселов. Эта процедура может строить и 1/4 окружности. Подробнее см. текст Приложения. Там же приведена более короткая подпрограмма, строящая 1/8 окружности методом Мичнера [], (том 1, стр. 152). Остальная часть окружности строится симметрично.
0.15 Приложение 4. Процедуры генерации окружности


В данном приложении помещены процедуры генерации окружностей по алгоритму Брезенхема и Мичнера, а также программа T_Circle для тестирования данных процедур.
Источник
Алгоритм Брезенхема для генерации окружности
Во многих областях приложений, таких как, например, системы автоматизированного проектирования машиностроительного направления, естественными графическими примитивами, кроме отрезков прямых и строк текстов, являются и конические сечения, т.е. окружности, эллипсы, параболы и гиперболы. Наиболее употребительным примитивом, естественно, является окружность. Один из наиболее простых и эффективных алгоритмов генерации окружности разработан Брезенхемом.
Для простоты и без ограничения общности рассмотрим генерацию 1/8 окружности, центр которой лежит в начале координат. Остальные части окружности могут быть получены последовательными отражениями (использованием симметрии точек на окружности относительно центра и осей координат).
Окружность с центром в начале координат описывается уравнением:
X 2 + Y 2 = R 2
Алгоритм Брезенхема пошагово генерирует очередные точки окружности, выбирая на каждом шаге для занесения пиксела точку растра Pi(Xi, Yi), ближайшую к истинной окружности, так чтобы ошибка:
была минимальной. Причем, как и в алгоритме Брезенхема для генерации отрезков, выбор ближайшей точки выполняется с помощью анализа значений управляющих переменных, для вычисления которых не требуется вещественной арифметики. Для выбора очередной точки достаточно проанализировать знаки.
Рассмотрим генерацию 1/8 окружности по часовой стрелке, начиная от точки X=0, Y=R.
Проанализируем возможные варианты занесения i+1-й точки, после занесения i-й.
При генерации окружности по часовой стрелке после занесения точки (Xi, Yi) следующая точка может быть (см. рис. 0.1а) либо Pg = (Xi+1, Yi) — перемещение по горизонтали, либо Pd = (Xi+1, Yi-1) — перемещение по диагонали, либо Pv = (Xi, Yi-1) — перемещение по вертикали.
Для этих возможных точек вычислим и сравним абсолютные значения разностей квадратов расстояний от центра окружности до точки и окружности:
|Dg| =| (X+1) 2 +Y 2 -R 2 |
|Dd|=| (X+1) 2 +(Y-1) 2 -R 2 |
|Dv|=| X 2 +(Y-1) 2 -R 2 |
Выбирается и заносится та точка, для которой это значение минимально.
Выбор способа расчета определяется по значению Dd. Если Dd 0, то диагональная точка вне окружности. Это варианты 5-7. И, наконец, если Dd = 0, то диагональная точка лежит точно на окружности. Это вариант 4. Рассмотрим случаи различных значений Dd в только что приведенной последовательности.
Случай Dd 2 + Y 2 — R 2 | — |(X+1) 2 + (Y-1) 2 — R 2 |
И будем выбирать точку Pg при di = 0 и Dd 2 + Y 2 — R 2 + (X+1) 2 + (Y-1) 2 — R 2 ;
Добавив и вычтя (Y-1) 2 получим:
di = 2 ·[(X+1) 2 + (Y-1) 2 — R 2 ] + 2·Y — 1
В квадратных скобках стоит Dd, так что
Ясно, что должен быть выбран горизонтальный пиксел Pg. Проверка компонент di показывает, что Dg 0
Здесь в качестве следующего пиксела могут быть выбраны или диагональный — Pd или вертикальный Pv.
Для определения того, какую пиксел выбрать Pd или Pv составим разность:
si = |Dd| — |Dv| = |(X+1) 2 + (Y-1) 2 — R 2 | — |X 2 + (Y-1) 2 — R 2 |
Если si 0, то выбираем вертикальный пиксел Pv.
Рассмотрим вычисление si для разных вариантов.
Для вариантов 5 и 6:
Dd > 0 и Dv 2 + (Y-1) 2 — R 2 + X 2 + (Y-1) 2 — R 2 ;
Добавив и вычтя (X+1) 2 получим:
si = 2 ·[(X+1) 2 + (Y-1) 2 — R 2 ] — 2·X — 1
В квадратных скобках стоит Dd, так что
Для компонент di имеем: Dg > 0 и Dd = 0, следовательно по критерию di > 0 выбираем диагональный пиксел.
С другой стороны, для компонент si имеем: Dd = 0 и Dv 0 — выбор диагонального пиксела Pd
si 0 — выбор вертикального пиксела Pv
выбор диагонального пиксела Pd.
Выведем рекуррентные соотношения для вычисления Dd для (i+1)-го шага, после выполнения i-го.
Для диагонального шага к Xi+1, Yi-1
Для вертикального шага к Xi, Yi-1
Источник