Растровый алгоритм Брезенхема построения линии
Важными характеристиками изображения являются:
- — количество пикселей. Может указываться отдельно количество пикселей по ширине и высоте (1024*768, 640*480. ) или же, редко, общее количество пикселей (обычно измеряется в мегапикселях);
- — количество используемых цветов (или глубина цвета);
- — цветовое пространство RGB, CMYK, XYZ, YCbCr и др.
Алгоритм Брезенхема (англ. Bresenham’s line algorithm) — это алгоритм, определяющий, какие точки двумерного растра нужно закрасить, чтобы получить близкое приближение прямой линии между двумя заданными точками. Это один из старейших алгоритмов в машинной графике — он был разработан Джеком Е. Брезенхемом (Jack E. Bresenham) в компании IBM в 1962 году. Алгоритм широко используется, в частности, для рисования линий на экране компьютера.
В алгоритме используется управляющая переменная di, которая на каждом шаге пропорциональна разности между s и t (см. рис.1). На рисунке 1 приведен i-ый шаг, когда пиксель Pi-1 уже найден как ближайший к реальному изображаемому отрезку, и теперь требуется определить, какой из пикселей должен быть установлен следующим: Ti или Si.
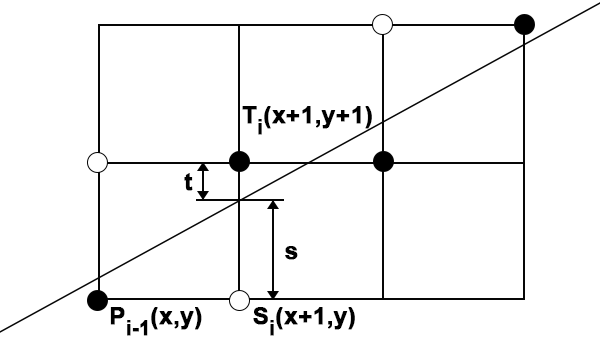
Рис.1
Из рисунка 1 следует, что
t = y + 1 — (Δy / Δx)(x + 1)
s — t = 2( Δy / Δx)(x + 1) — 2y — 1.
Домножим обе части равенства на Δx:
Δx(s — t) = 2(Δy•x — y•Δx) + 2Δy — Δx.
Так как Δx > 0, то величину Δx(s-t) можно использовать в качестве критерия для выбора пикселя. Обозначим эту величину di:
Так как di надо считать на каждом шаге, рассчитаем величину Δi — приращения di:
Если di = 0, а потому при перемещении точки изменяли значение на +1. Если значение Δy Войдите или зарегистрируйтесь, чтобы комментировать
Источник
Алгоритм рисования толстых линий
На этом шаге мы рассмотрим несколько алгоритмов вывода таких линий .
Для описания различных по виду изображений на основе линий используют термин стиль линий или перо . Термин перо иногда делает более понятной суть алгоритма вывода линий для некоторых стилей — в особенности для толстых линий. Например, если для тонкой непрерывной линии перо соответствует одному пикселю, то для толстых линий перо можно представить себе как фигуру или отрезок линии, который скользит вдоль оси линии, оставляя за собой след.
Взяв за основу любой алгоритм вывода обычных тонких линий (например, алгоритм Брезенхэма), запишем его в следующем обобщенном виде:
Можно представить себе такой алгоритм, как цикл, в котором определяются координаты (х,у) каждого пикселя. Этот алгоритм можно модифицировать для вывода толстой линии следующим образом:
Вместо вывода отдельного пикселя стоит вывод фигуры или линии, соответствующей перу — прямоугольник, круг, отрезок прямой.
Такой подход к разработке алгоритмов толстых линий имеет преимущества и недостатки. Преимущество: можно прямо использовать эффективные алгоритмы для вычисления координат точек линии оси, например, алгоритмы Брезенхэма. Недостаток: неэффективность для некоторых форм пера. Для перьев, которые соответствуют фигурам с заполнением, количество тактов работы алгоритма пропорционально квадрату толщины линии. При этом большинство пикселов многократно закрашивается в одних и тех же точках (рисунок 1).
Рис.1. Прямоугольное и круглое перья работают избыточно
Такие алгоритмы более эффективны для перьев в виде отрезков линий. В этом случае каждый пиксель рисуется только один раз. Но здесь важным является наклон изображаемой линии. Ширина пера зависит от наклона (рисунок 2).
Рис.2. Перья в виде отрезков линий
Очевидно, горизонтальное перо не может рисовать толстую горизонтальную линию.
Для вывода толстых линий с помощью пера в качестве отрезка линии чаще всего используются отрезки горизонтальной или вертикальной линий, реже — диагональные отрезки под углом 45 градусов. Целесообразность использования такого способа определяется большой скоростью вывода горизонтальных и вертикальных отрезков прямой. Для того чтобы достигнуть минимального количества тактов вывода, толстые линии, которые по наклону ближе к вертикальным, рисуют горизонтальным пером, а пологие линии — вертикальным пером.
При выводе толстых линий с использованием пера-отрезка линии заметны разрывы в углах полилиний и плохие концы (рисунок 3).
Рис.3. Вывод толстых линий с использованием пера-отрезка
Для решения таких проблем иногда используют другие алгоритмы вывода толстых линий. Например, вывод толстой полилинии можно выполнить как рисование полигона с заполнением (рисунок 4).
Рис.4. Пример толстой полилинии
Очевидный недостаток такого подхода — меньшая скорость вывода, поскольку заполнение полигона — это существенно более трудоемкая задача, чем вывод линий, а кроме того, нужно еще определять координаты его вершин.
Третья разновидность алгоритмов вывода толстых линий — рисование толстой линии последовательным наложением нескольких тонких линий, смещенных одна относительно второй.
На следующем шаге мы рассмотрим вывод пунктирной линии .
Источник
Курс «Рисовать просто» урок №3 «Линии и штрихи»
Урок 3
Линии и штрихи
Надеюсь, все заточили карандашики
Сегодня начинаем практиковаться.
Впереди еще много теории, но чтобы выполнять следующие задания, вам нужно уверенно держать карандаш в руке и уметь штриховать.
А единственный способ этому научиться–практика. Сегодня покажу несколько упражнений, выполняя которые ежедневно (хотя бы по 10-15 мин) вы сможете почувствовать карандаш и не бояться провести линию.
Не пренебрегайте упражнениями. Это именно те азы, без которых невозможно потом красиво и легко рисовать.
Для тренировки можно использовать обычную офисную бумагу и карандаш ТМ.
Обратите внимание, как я держу карандаш (на видео). Он должен свободно лежать в руке. Не давите сильно на бумагу. На ней не должно оставаться борозд от ваших штрихов.
Старайтесь опираться на бумагу только лишь мизинцем, а не возить ладонью по листу.
Итак, поехали :
1. Рисуем на небольшом участке каракули . стараемся заключить их в какую-то определенную форму, например в прямоугольник.
2. Прямые вертикальные линии. Рисуем линии снизу вверх одинаковой длины на равном расстоянии друг от друга. Подобным упражнением мы тренируем не только руку, но еще и глаза.
3. Далее проделывает тоже самое в разных направлениях: сверху вниз, по диагонали под разным углом, горизонтальные, сетка. Во всех случаях стараемся делать так, чтобы линии были ровными, параллельными друг другу, на одинаковом расстоянии друг от друга.
Ну как? Получается?
Если не очень, то не расстраиваемся, а просто практикуемся дальше. Со временем рука привыкает и ваши линии станут идеальными!
4. Рисуем зигзаги. Сначала из прямых линий, затем зигзаг с петлями. Следим за стройностью наших рядов.
5. Спирали. Рисуем спирали по часовой стрелке, затем против часовой стрелки, из центра, с внешнего края. Стараемся получить круглую спираль, а не бесформенное нечто. (первая спираль у меня как раз и получилась — нечто.как говорится : и на старуху бывает проруха.
6. Кружочки. Рисуем ровные ряды небольших кружочков. И можно в каждый из них в центр поставить точечку. Проверяем свой глазомер.
И готовим руку к штриховке:
Упражнение «Черный квадрат»
Пробуем нарисовать темный квадрат. Рисуем очень частые штрихи в одном направлении: не туда-сюда, а именно только сверху-вниз, или снизу-вверх.
(Смотрим видео внизу)
Затем рядом рисуем еще один такой же квадрат, дополняя его слоем из горизонтальных штрихов также в одном направлении.
И последний наш квадрат будет состоять из трех слоев штрихов: вертикально, горизонтально и по диагонали.
Нажим на карандаш делаем легкий. Наша задача добиться интенсивности цвета количеством слоев и пересечениями штрихов, а не тем, с какой силой вы давите на карандаш.
Думаю на сегодня достаточно)
P.S. еще видео о том, как правильно штриховать и как НЕ правильно
Штрихи должны быть отдельными линиями, а не сплошными каракулями. Держим карандаш примерно за серединку, а не у самого кончика и под углом (около 45 градусов) к бумаге.
Домашнее задание:
Тренируйте вашу руку каждый день – и будет вам счастье))) Повторяем все эти упражнения, независимо от того идеально ли у вас получилось с первого раза или никак линии не выстраиваются ровными рядами.
Если есть вопросы по заданию –пишем в комментариях.
Источник
Целочисленная линия: Алгоритм Брезенхема
В материале про Сапёра мы обсудили преимущества рисования горизонтальных линий, но очевидно, что одними горизонтальными линиями все задачи не решить. Ведь часто требуется рисовать линии под любым углом.
Есть готовые библиотечные методы рисования линий. Зачем нам делать это вручную? Во-первых, для упражнения, чтобы понять математическую основу. Во-вторых, нам может потребоваться рисовать линию, где каждый пиксел надо обработать по-своему. В-третьих, линию необязательно рисовать на экране. Она может понадобиться и для других задач в виде просто набора данных, так что библиотечный метод, который рисует на экране, нам не поможет.
Как вообще нарисовать линию
Для порядка уточним, что мы рисуем отрезки, у которых есть начало (x0, y0) и конец (x1, y1).
Рассмотрим тривиальный случай – горизонтальную линию. Например, её длина равна 100 пикселов. Значит, надо начать с координат (x0, y0) и сделать цикл на 100 повторений, и в каждом шаге цикла просто увеличивать координату «x» на 1.
Теперь рассмотрим такую же линию, но под наклоном. В ширину она занимает 100 пикселов, а в высоту 50.
По сути задача не изменилась: мы точно так же делаем цикл на 100 повторений, и прибавляем к координате «x» по 1. Но теперь мы должны прибавлять что-то и к координате «y». Если ширина и высота линии относятся как 100:50, значит, когда мы к «x» прибавляем 1, то к «y» должны прибавлять 0.5. Ну то есть в общем случае:
Если шаг по «x» это 1, то шаг по «y» это 1 * (dy/dx).
Можно посмотреть онлайн , линии генерируются при каждом перезапуске:
Как видим, не всё хорошо: если dx dy, то двигаемся по «x», а иначе по «y». Это будет сделано ниже, а пока –
Почему это порождало проблемы?
Рассмотрим вариант, когда к «y» прибавляется 0.5. Это дробное число, а пикселы на экране целые. Мы не можем закрасить 0.5 пиксела.
Стоп, но вот же в примере выше нарисованы линии с дробной координатой «y» и всё прекрасно. В чём проблема?
Пикселы здесь рисуются с помощью библиотечного метода рисования прямоугольника (каждый пиксел по факту это маленький квадратик), и когда мы передаём туда дробные координаты, они автоматически округляются. Кроме того, библиотечный метод, когда видит дробную координату, сглаживает края квадрата, заменяя чёрный цвет на градации серого.
Вот так линии будут выглядеть, если мы сами начнём округлять координаты, и сглаживания тогда происходить не будет:
В общем, проблема – в вещественной арифметике, которая во-первых требовала постоянного округления, а во-вторых, на старых процессорах вообще работала медленнее, чем целочисленная (говорят, что сейчас это уже не так).
Как бы то ни было, алгоритм Брезенхема позволяет построить данные для линии, используя только целые числа и только сложение или вычитание, без умножения и деления.
Именно поэтому в прошлом он был абсолютно необходим всем, кто занимался компьютерной графикой. Думаю, что будет интересен и сейчас.
В его основе лежит принцип накопления ошибки. Познакомившись с ним, вы сможете применять его не только для рисования линий, но и для других задач.
Реализация алгоритма Брезенхема
Реализацию на JavaScript вы можете посмотреть онлайн , а здесь будут пояснения. Самое первое – при рисовании линии c шириной dx и высотой dy мы всегда нарисуем не более чем dx или dy пикселов (смотря что из них больше). Например, линия задана координатами (100,100)–(200,150). Значит, по «x» она занимает 100 пикселов, а по «y» 50 пикселов. Значит, мы нарисуем 100 пикселов, расположенных вдоль координаты x.
1. Выяснить наибольшую дистанцию
Так как конец отрезка может находиться и левее-правее, и выше-ниже начала, то dx или dy могут получиться отрицательные. Чтобы узнать, кто больше, надо взять их абсолютные значения. Мы сохраним их в переменных dist_x и dist_y :
dx = x1 — x0;
dy = y1 — y0;
dist_x = Math.abs(dx);
dist_y = Math.abs(dy);
Затем заводим переменную dist , которая хранит максимальную из двух дистанций:
dist = dist_x;
if (dist_y > dist_x) dist = dist_y;
В нашем примере она будет равна 100.
2. Отказ от дробных чисел
После первого пункта мы уже точно знаем, что будем двигаться по координате «x» с приращением 1. Приращение по «y» равно 1 * (dy/dx) = 0.5.
Координаты (x,y) сразу целочисленные, так как иначе нет смысла использовать этот алгоритм. Добавляя 1 к координате «x», мы увеличиваем её ровно на 1, здесь всё работает нормально. Но добавляя 0.5 к «y», мы не увеличиваем её ни на сколько – целое число остаётся целым. То есть приращение по «y» работать не будет.
Как исправить эту проблему, сохранив координаты целочисленными?
В качестве временной меры заведём переменную-накопитель для координаты «y»: err_y . Пусть она пока будет вещественного типа. Теперь мы можем добавлять 0.5 не к координате «y», а к накопителю. Как только накопитель станет больше либо равен 1, мы получили целое смещение. Тогда мы уже законно прибавим 1 к «y», и отнимем 1 от накопителя, чтобы он мог снова накапливать.
Теперь надо сделать сам накопитель целочисленным. Сейчас пороговым значением, когда срабатывает накопитель, является 1.
Берём во внимание тот факт, что 0.5 во столько же раз меньше 1, во сколько раз расстояние dy меньше dx . Собственно говоря, иначе и быть не может, так как само приращение по «y» вычисляется из отношения dy/dx .
Следовательно, пороговым значением можно сделать не 1, а dist . И тогда к накопителю err_y прибавляем уже не 0.5, а dist_y . Накопитель будет расти в той же самой пропорции, в какой рос при приращении 0.5 и пороге 1. Как только он превышает порог ( dist ), мы прибавляем 1 к координате «y» и вычитаем dist из накопителя. Таким образом, мы получили целочисленный накопитель, который работает идентично вещественному.
2. Установить шаги приращения координат.
И координата «x», и координата «y» всегда изменяются с шагом 1. Потому что меньше пиксела нельзя, а больше – будут разрывы . На каждом шаге цикла прирастает либо «x», либо «y», либо обе координаты. Но также как и dx , dy , эти приращения могут быть отрицательными. Определим их правильно и занесём в переменные step_x , step_y :
3. Накопители ошибок
Мы уже сделали накопитель err_y для оси «y», сделаем то же самое для оси «x»: err_x , ведь отношение сторон не всегда будет такое, как в нашем примере, и значит, для «x» понадобятся такие же расчёты.
4. Рисование линии
Делаем цикл на dist повторений, так как мы уже знаем, что нужно нарисовать ровно dist пикселов.
Тут мы уже не делаем предположений, что dist_x больше чем dist_y или наоборот. Мы просто в каждом шаге прибавляем к накопителю err_x значение dist_x , а к err_y значение dist_y . Как только один из накопителей превысил порог dist , мы вычитаем из него dist , и прибавляем к соответствующей координате её шаг.
И вот что выходит. Один из накопителей ВСЕГДА будет точно достигать порога dist при каждом шаге. Потому что dist равна либо dist_x , либо dist_y . Допустим, dist_x > dist_y , тогда dist = dist_x , и прибавляя к накопителю err_x значение dist_x , мы мы всегда будем точно достигать dist , и значит, «x» будет прирастать на 1 в каждом шаге цикла. А err_x будет сбрасываться точно в ноль.
А что происходит с err_y ? К нему прибавляется dist_y , то есть 50. И на первом шаге err_y будет меньше, чем dist . Значит, мы сдвинемся по «x», но не сдвинемся по «y».
На втором шаге мы опять сдвинемся по «x», и увеличим err_y ещё на 50. Теперь err_y == dist , и значит, можно прибавить шаг к координате «y» и вычесть dist из err_y .
Значит, «x» будет прибавляться каждый шаг, а «y» – через один шаг. Cобственно так и должно быть при пропорциях линии 2:1.
Мы получим такую линию:
Если взять другую линию, где dy = 100 и dx = 50 , то теперь dist будет равна dist_y , и уже «y» начнёт прирастать каждый шаг, а «x» через шаг.
А где же накапливается ошибка?
В примере у нас соотношение сторон 2:1. Это значит, что высота укладывается в ширину ровно два раза, и тогда линия рисуется как лестница со ступеньками шириной в 2 пиксела. То же самое можно сказать про отношения 1:1, 3:1, 4:1, 5:1 и т.д. Везде высота укладывается в ширину целое число раз, и поэтому все ступеньки линии будут одинаковой длины.
Но можно взять другие размеры линии, например, dx = 100 , dy = 63 . Тогда каждая ступенька линии должна быть длиной 1.587 пиксела. Это уже не целое число, и мы возвращаемся к проблеме, когда мы не можем закрасить часть пиксела.
Но посмотрим, как работает алгоритм:
На первом шаге err_y = 63 . На втором шаге err_y = 126 . Это больше 100, поэтому вычитаем 100 и остаётся 26. Этот остаток и есть ошибка. Это величина, на которую err_y превысило порог. Можно считать его дробной частью пиксела. В следующий раз добавляем 63 и получаем 89, добавляем ещё 63 и получаем 152. Вычитаем 100, остаётся 52 – ошибка выросла. Добавляем 63, получаем 115. Вычитаем 100, остаётся 15 – ошибка снизилась.
Каждый остаток идёт в зачёт для следующего пиксела. То есть дробные части пикселов мы не обнуляем, а накапливаем. Это похоже на механизм високосного года: каждый месяц набегает небольшое количество лишнего времени, и все эти погрешности за 4 года складываются в один лишний день. На практике это выглядит так: линия состоит из ступенек, допустим, по 3 пиксела. Но вдруг где-то появляется ступенька в 2 пиксела. Потом опять 3, а потом опять 2. И линия будем выглядеть примерно так:
Таким образом, нецелые соотношения заставляют длину ступенек время от времени меняться. Разная длина ступенек это и есть следствие накопления ошибки.
Общая мораль такова: если работаете с целыми числами, то не обнуляйте, а накапливайте погрешность.
Источник








